EL Rincón de Yanka: LA BELLEZA NUMÉRICA DEL UNIVERSO

LA BELLEZA NUMÉRICA DEL UNIVERSO

En el siglo XIII, Santo Tomás de Aquino formuló una de las verdades fundamentales de la estética: “Los sentidos se deleitan con las cosas debidamente proporcionadas”. Y nada en la naturaleza es tan pequeño o insignificante que no merezca un agradable toque de simetría o asimetría, que aumente su perfección y belleza.

El número de oro y sus derivados son la clave de la belleza y la singularidad del mundo que nos rodea. Está presente en las flores, en los animales y en los humanos.

Podemos definir la belleza de una manera escueta, con un solo número: el número áureo, llamado Φ en honor de Fidias (que en griego antiguo se escribe Φειδίας), sin duda el mejor arquitecto y escultor de la Atenas clásica.

Existen muchísimos ejemplos de fantásticas simetrías o asimetrías, como son los innumerables y hermosos hexágonos de los copos de nieve, la hermosa espiral geométrica del caracol de mar, los formas perfectas que se encuentran en los cristales minerales, y así podríamos seguir citando tantos y tantos aspectos de la naturaleza.

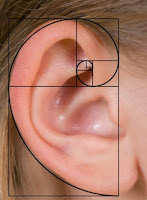
Tras esa belleza de muchos de los elementos naturales que nos rodean, está una serie matemática conocida como Sucesión de Fibonacci, alias del matemático italiano Leonardo de Pisa (1170-1250). Esta sucesión es posiblemente una de las sucesiones numéricas más conocidas, dadas las propiedades que posee y la gran cantidad de veces que aparece, en asuntos que aparentemente no tienen relación entre sí. De la sucesión de Fibonacci deriva por ejemplo la famosa Proporción Dorada o Número Áureo, que está presente muy frecuentemente en temas relacionados con la arquitectura, el arte o la propia naturaleza.

La serie numérica de Fibonacci se obtiene comenzando por los dos primeros números, 0 y 1, y después cada número de la serie se obtiene sumando los dos que le preceden, con lo que resulta:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, …

Empecemos por una definición individual de cada uno de estos conceptos:

Sucesión de Fibonacci. Partiendo desde el número uno, la sucesión de Fibonacci consiste en ir sumando el resultado de la última operación con su mayor sumando. Es decir: 0+1=1, 1+1= 2, 1+2=3, 2+3=5, 3+5=8, y así sucesivamente.

El segmento áureo. Es un segmento dividido en dos partes de forma que se cumple la igualdad (a+b)/a = a/b, donde (a+b) es el total del segmento, ala parte más grande y b la parte de menor tamaño.

Número áureo (de oro). Conocido desde hace siglos, el número de oro –también llamado número fi o número áureo– está asociado a la belleza y a la naturaleza. Se representa con la letra griega “phi” (φ), se pronuncia “fi” y su valor es 1.61803398874989… Se trata de un número irracional, pues cuenta con infinitos números decimales no periódicos.

Una vez conocidos estos tres conceptos, es hora de relacionarlos entre sí.

Sucesión de Fibonacci y el número de oro. Si dividimos dos números consecutivos de la sucesión de Fibonacci, obtenemos un cociente muy próximo al número de oro. Conforme más elevados sean los número de la sucesión de Fibonacci, el cociente se irá aproximando cada vez más al valor óptimo del número de oro. Por ejemplo: 8/5 = 1.6, pero 1597/987 = 1,6180344478, el cual se aproxima aun más al 1.61803398874989 determinado como número áureo.

El segmento áureo y el número de oro. La relación existente entre los términos a y b en la ecuación (a+b)/a = a/b que determina los segmentos áureos, es, precisamente, el número áureo. Es decir, si dividimos a/b o realizamos (a+b)/a, obtendremos el número de oro. Es por esto por lo que el número de oro también es conocido como proporción áurea o número áureo. De la misma forma, el segmento áureo y sus derivados deben su nombre a esta proporcionalidad.

La influencia del número áureo en el mundo que nos rodea.

La sucesión de Fibonacci, la proporción áurea y sus derivados (como la espiral de Fibonacci) están presentes en la naturaleza y son considerados estándares de belleza, singularidad e inteligencia. Se puede ver, por ejemplo, en:

Las galaxias y los agujeros negros.

Los edificios.

Flores como las rosas o los girasoles.

En animales como los moluscos.

En los huracanes.

En el arte y en los seres humanos.

En logotipos.